第一周
有关训练、验证、测试集的分配问题,在早期的机器学习中,由于数据规模不大,所以一般是7/3分,也就是70%验证集(dev set)加上30%测试集,没有明确验证集的话也可以采用60%训练、20%验证以及20%测试划分。不过目前进入了大数据时代,我们所需要测试集和验证集的比例可以大幅缩小,因为它们的作用是对参数进行调整和验证,所以我们应该对确立模型的训练集加大数量。
高偏差(high bias)—欠拟合(underfitting)
高方差(high variance)—过拟合(overfitting)
欠拟合:在训练数据和未知数据上表现都很差。
解决方法:采用更复杂的网络、减少正则化参数、添加其他特征项。
过拟合:在训练数据上表现良好,但是在未知数据上表现差。
解决方法:采用更多的训练数据、正则化、清洗数据、数据增强(比如反转图片、增加干扰)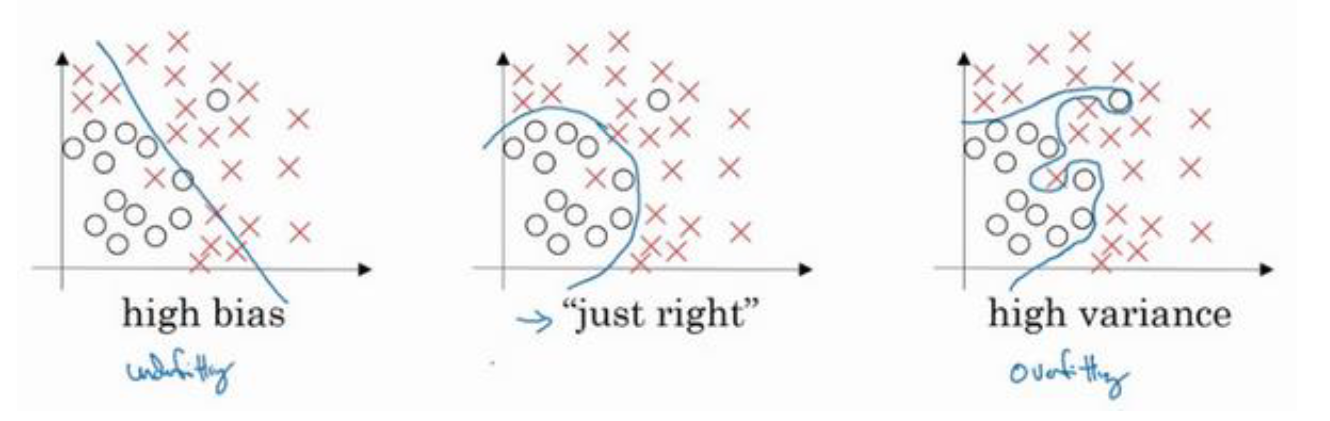
训练集误差小,验证集误差大,则可能是过度拟合了训练集,而验证集没有充分发挥作用,这就是高方差和过拟合。
训练集误差大,验证集误差小,则可能连训练集都无法拟合,这就是高偏差和欠拟合。
训练集误差大,验证集误差更大,这就是高偏差和高方差的情况,是最坏的一种情况。
训练集误差小,验证集误差小,这就是低偏差和低方差的情况,是比较理想的一种情况。
还有一点就是贝叶斯误差,这一般是指人眼能够分辨出的误差,如果贝叶斯误差比较大,而同时分类器给出的训练误差与验证误差都与这个贝叶斯误差接近,那么这其实说明是非常合理的情况。解决过拟合问题的方法一般是正则化或者准备更多的数据,但鉴于准备足够多的数据具有相当难度,所以一般使用正则化解决这个问题。
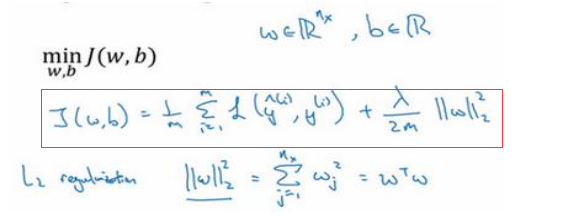
一般正则化的写法就是在代价函数后加上参数的范数。
范数是指某个向量空间或者矩阵中的每个向量的大小或者长度。其定义如下: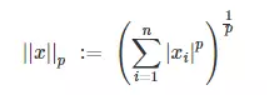
也就是说L1范数是指某个向量中所有元素绝对值的和,这也就是L1正则化,它的好处是产生稀疏矩阵,也就是w向量中存在很多0。L2范数是指某个向量中所有元素平方的和再开根,即欧几里得距离。目前人们越来越倾向于使用L2正则。同时这个L2范数也被称为弗罗贝尼乌斯范数(Frobenius norm),而L2正则化这个操作被称为权重衰减(weight decay)。为什么L2正则化能够减少过拟合的影响?
这是因为在更新学习率的过程中,我们对w参数的调整是w:=w-αdw,正则化就是改变这个dw。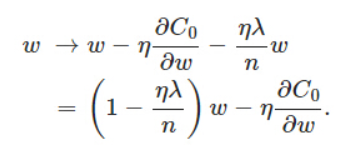
正则化之后w的参数前有了(1-ηλ/n),由于这三个参数都是正数,所以必然小于1,这就让w这个参数衰减了,虽然其实最终w的结果还得取决于后面ηdw的值。过拟合情况的发生意味着拟合函数的系数非常大,因为它需要去尽量拟合每一个点,所以正则化的作用就是通过约束参数的范数使其不要太大,可以在一定程度上减少过拟合情况。Dropout正则化
Dropout是指在深度网络训练的过程中,对于某些神经网络单元,按照一定的概率暂时将其从网络中丢弃。它之所以对过拟合有帮助,那时因为Dropout情况下,权值的更新不再依赖于有固定关系的隐含节点的共同作用,因为这些节点可能随时被暂时舍弃,要弥补这个损失,需要除以keep_prob参数用于平衡。归一化
归一化的作用是为了能让梯度下降更加顺利,如果不进行归一化,有可能会导致值的分布极为分散而影响梯度下降的效率。梯度爆炸和梯度消失
这里指的就是参数W的矩阵如果它的值大于1则可能在经过非常深的网络之后导致梯度指数级增长,达到爆炸的效果,反之若小于1,则有可能在深层网络中指数级减小,达到消失的效果。